Abstract
Multiparticle correlators are mathematical objects frequently encountered in quantum field theory and collider physics. By translating multiparticle correlators into the language of graph theory, we can gain new insights into their structure as well as identify efficient ways to manipulate them. In this paper, we highlight the power of this graph-theoretic approach by “cutting open” the vertices and edges of the graphs, allowing us to systematically classify linear relations among multiparticle correlators and develop faster methods for their computation. The naive computational complexity of an N-point correlator among M particles is $\mathcal O(M^N)$, but when the pairwise distances between particles can be cast as an inner product, we show that all such correlators can be computed in linear $\mathcal O(M)$ runtime. With the help of new tensorial objects called Energy Flow Moments, we achieve a fast implementation of jet substructure observables like $C_2$ and $D_2$, which are widely used at the Large Hadron Collider to identify boosted hadronic resonances. As another application, we compute the number of leafless multigraphs with $d$ edges up to $d=16\ (15,641,159)$, conjecturing that this is the same as the number of independent kinematic polynomials of degree d, previously known only to $d=8\ (279)$.
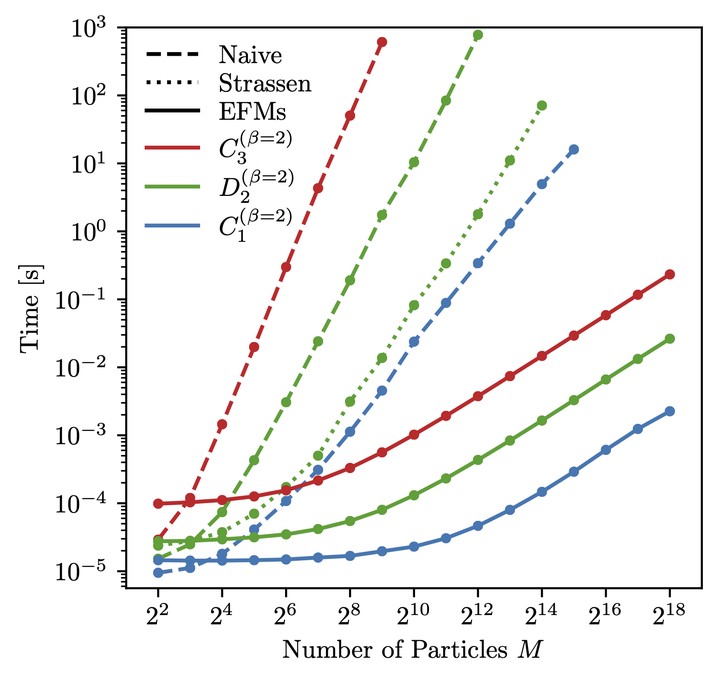
Figure 1: Time to compute three jet substructure observables as a function of the number of particles. The EFMs show the expected linear scaling, which is signficantly faster than other methods, including fast matrix multiplication for the $D_2$ observable.

Table IV: Number of multigraphs with $d$ edges that have no vertices with only one edge (i.e. are leafless), for both connected and all graphs. These sequences have been added to the Online Encyclopedia of Integer Sequences (OEIS) as A307317 and A307316. We conjecture that the sequence for all graphs is the same as A226919 which was discovered in the context of counting the number of independent, symmetric kinematic polynomials up to momentum conservation, a problem which arises in the enumeration of certain string theory amplitudes. The leafless property of the graphs is related to the momentum conservation of the kinematic quantities in the polynomial picture. Our method allows for signficantly faster enumeration, and the values for $d>8$ (bolded) are new results.