Energy Flow Polynomials: A complete linear basis for jet substructure

Abstract

We introduce the energy flow polynomials: a complete set of jet substructure observables which form a discrete linear basis for all infrared- and collinear-safe observables. Energy flow polynomials are multiparticle energy correlators with specific angular structures that are a direct consequence of infrared and collinear safety. We establish a powerful graph-theoretic representation of the energy flow polynomials which allows us to design efficient algorithms for their computation. Many common jet observables are exact linear combinations of energy flow polynomials, and we demonstrate the linear spanning nature of the energy flow basis by performing regression for several common jet observables. Using linear classification with energy flow polynomials, we achieve excellent performance on three representative jet tagging problems: quark/gluon discrimination, boosted W tagging, and boosted top tagging. The energy flow basis provides a systematic framework for complete investigations of jet substructure using linear methods.

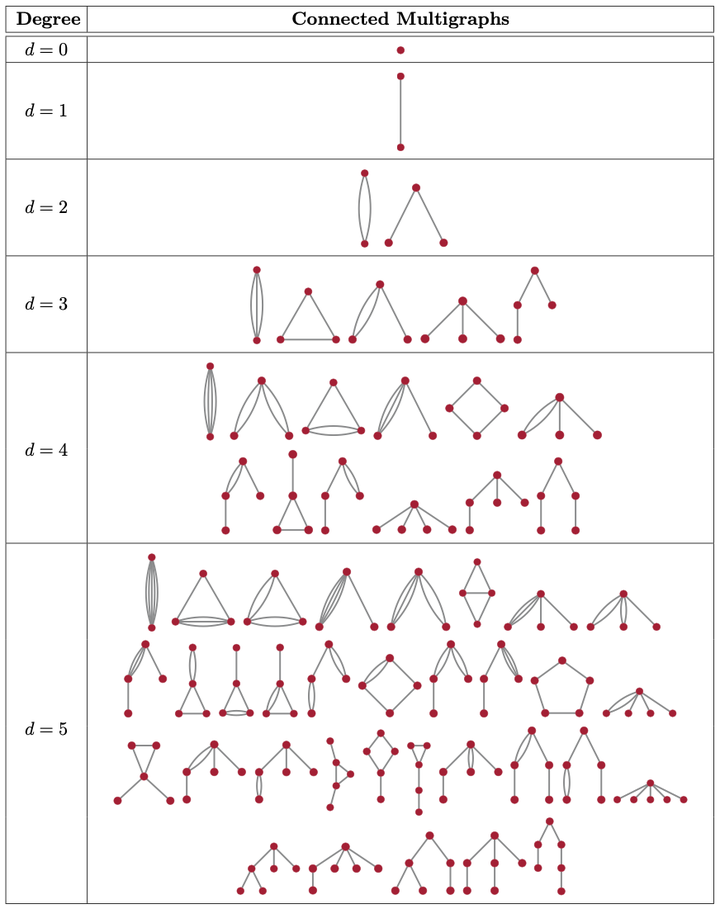
Table 3: The Energy Flow Polynomials (EFPs) are in one-to-one correspondence with the set of non-isomorphic, loopless multigraphs. This graphical picture provides an extremely useful language for manipulating and using EFPs and related quantities (such as the EFMs.) We organize the EFPs by their degree, or the number of edges in the graph, shown here for connected graphds up to $d=5$.

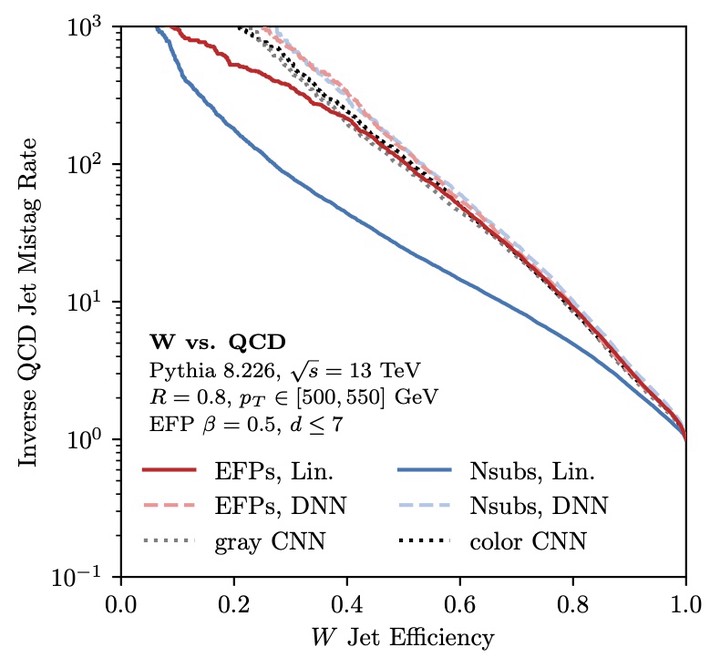
Figure 7: ROC curves for classifying W-boson jets from QCD-initiated jets using a variety of methods. Amazingly, a linear classifier trained with EFPs is able to compete with a state-of-the-art deep convolutional neural network (CNN) using jet images. This provides strong empirical support that the EFPs are a practical linear basis for any IRC-safe quantity.