Abstract
We establish that many fundamental concepts and techniques in quantum field theory and collider physics can be naturally understood and unified through a simple new geometric language. The idea is to equip the space of collider events with a metric, from which other geometric objects can be rigorously defined. Our analysis is based on the energy mover’s distance, which quantifies the “work” required to rearrange one event into another. This metric, which operates purely at the level of observable energy flow information, allows for a clarified definition of infrared and collinear safety and related concepts. A number of well-known collider observables can be exactly cast as the minimum distance between an event and various manifolds in this space. Jet definitions, such as exclusive cone and sequential recombination algorithms, can be directly derived by finding the closest few-particle approximation to the event. Several area- and constituent-based pileup mitigation strategies are naturally expressed in this formalism as well. Finally, we lift our reasoning to develop a precise distance between theories, which are treated as collections of events weighted by cross sections. In all of these various cases, a better understanding of existing methods in our geometric language suggests interesting new ideas and generalizations.
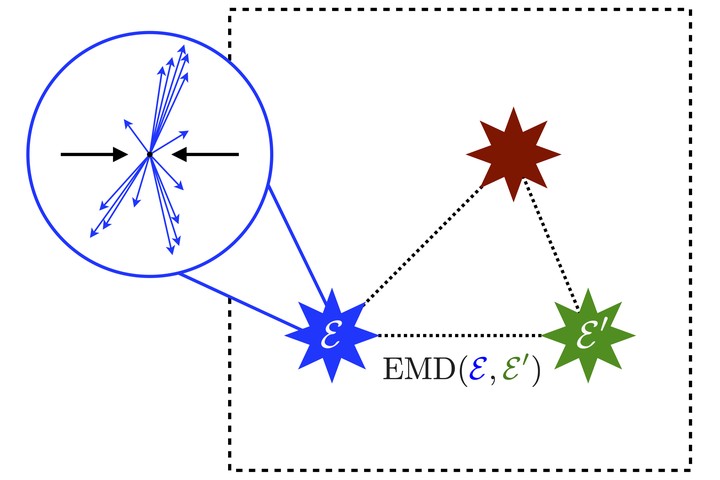
Figure 1: An illustration of the space of events. Each point in the dashed black region represents an event, which is a collection of particles that each have energies and directions. The Energy Mover’s Distance (EMD) measures the distance between events.
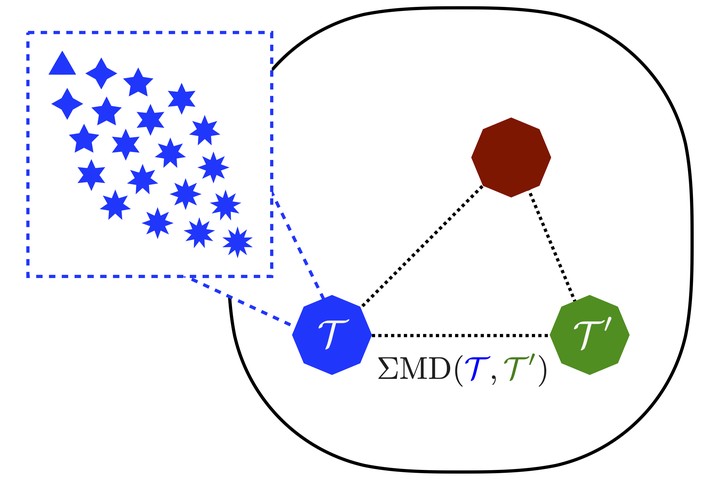
Figure 10: An illustration of the space of theories, analogous to the space of events. Each point in the enclosed region represents a theory, which is a collection of events, which each consist of sets of particles. The Theory Mover’s Distance ($\Sigma$MD) measures the distance between theories, analogous to how the EMD measures the distance between events.
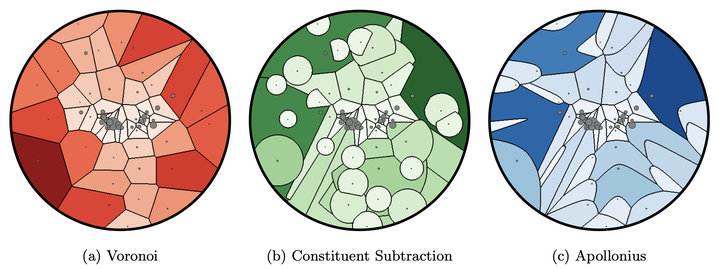
Figure 9: A depiction of three pileup mitigation algorithms acting on the same example jet from the CMS 2011A Open Data. Each particle receives a correction to its transverse momentum proportional to the are of its region. The Apollonius graph has the property that it minimizes the EMD between the jet and the uniform radiation that represents the pileup that is being subtracted away.